This guide assumes that the reader is clear with Java language basics, hence just giving the basic idea of each listed topic and links to interview questions for each topic is given at the end of synopsis.
To prepare for the interview a lot of coding practice is required and basics must be clear, so once done with any topic try to write some code and check output, post comments and discuss if any difficulty.
Object oriented design principles
While dealing with OOPS one should know about important principles related to OOPS.
Encapsulation,Inheritance,Polymorphism are main principles related to OOPS. While looking at open source code we can see a lot of design patterns such as Singleton pattern, Factory pattern etc, but first one should command over the basic principles. Listing these principles here one by one:
Encapsulation
Definition : Encapsulation is the process to bind code and data together.
By binding code and data together means we have certain set of rules through which data can be accessed and modified. In case of Java a class contains data(variables) and methods to operate on that data and binding that data means that code can be accessed through well defined method signature.
By specifying access modifiers(public, private,default) we restrict access to data within a class, marking a method private will restrict access for other objects outside the class, hence hiding the complexity and providing abstraction.
Inheritance
Definition : Inheritance is the process by which one object acquires properties of another object.
Inheritance describes a hierarchical approach in which a subtype inherits the properties defined by its super-type.
In Java using interfaces and programming to interfaces makes programs much easier to maintain and provides more abstraction while making use of inheritance.
Inheritance also make uses of encapsulation,for example: data members of a super class defined as private are not visible to its subclasses.
Polymorphism
Definition : Polymorphism means one name multiple aspects.
In Java polymorphism is implemented mainly in two forms:
1. Overloading -- Same method name but different signature (
static polymorphism)
2. Overriding -- Same method name and same signature (subclass overrides method from super class) (
dynamic polymorphism)
Overloading deals with the same method name but different signature, for example:
public void fun(int a){ //do something }
public void fun(String str){ //do something }
The thing to keep in mind is,
at compile time reference variable decides which method will be invoked but at run time actual object decides which method to invoke
. This process is known as virtual method invocation or dynamic dispatch.
For example:
class Employee{
public void print(){
System.out.println("Inside employee");
}
}
class Developer extends Employee{
public void print(){
System.out.println("Inside Developer");
}
}
class Main{
public static void main(String[] arg){
Employee emp = new Employee();
Employee dev = new Developer();
emp.print(); //prints :Inside employee
dev.print(); //prints :Inside Developer
}
}
So at compile time both the calls to print checks the reference variable, since reference variable is same in both cases, compiler will know that method in Employee class is being called, but at the run time actual object determines which method to invoke, hence method in Developer gets invoked in second case.
Classes and Object fundamentals
Points to note:
1. A constructor always invoked when a new object is created, and the call goes all the way up to Object class through inheritance hierarchy.
2. Instance members are accessible only after call to super completed.
3. Static members (methods and variables) belong to a class.
4. Static block(s) gets executed only once when the class is loaded. Static blocks gets executed in the order they are declared.
5. Static can't refer 'this' and 'super'.
6. To instantiate an object all instance variables in class and it's superclass must be initialized first.
7. While creating a new object, order of invocation will be: complete super class instance variable invocation -> complete super class constructor invocation -> complete own instance variable invocation ->complete own constructor invocation.
Exceptions
Exception: An exception is an event which disrupts the normal flow of the program. Exceptions are objects in Java
 |
| Figure : Exception Hierarchy |
Java supports exception mechanism in which two types of Exceptions exists
1.
Checked exceptions: Exception and its subclasses other than RuntimeException and its subclasses comes into checked exception category.
Handle or declare strategy states that either handle the exception using try-catch-finally block or declare using throws keyword.
Checked exceptions are exceptions which strictly follows handle or declare strategy. By marking an exception checked one must need to surround it using try-catch-finally or use throws keyword.
Eg: IOException
2.
Un-checked exceptions: Subtypes of Error and RuntimeException comes into unchecked exception category.
Any unchecked exception need not to be handled or declared. As a programmer one can handle/declare it but compiler won't complain in case its NOT handled or declared.
Eg: ArrayIndexOutOfBoundException
Finally block:
finally block ALWAYS executes, except in following cases.
* If the JVM exits while the try or catch code is being executed, then the finally block may not execute.
* Likewise, if the thread executing the try or catch code is interrupted or killed, the finally block may not execute even though the application as a whole continues.
* Finally block overrides any exception or return statement in try/catch block, it means if there is any return statement or exception in catch block finally will still execute.
String
String objects are immutable.That means once a String object is created it can't be changed.
Any operation on String object returns a new object.
String literals are kept in String constant pool, whenever a new String literal created compiler checks in the pool whether it already exists, if it does, then reference points to existing literal.
For example:
String str="Hello"; // a string object created and placed in string pool
String st=new String("Hello"); //here 2 objects created,
/**
a new string object created and placed in non pool memory
and a literal "Hello" will be placed in string pool.
Invoking any method on string object will create new object.
**/
eg: str= str.toUpperCase();
/**
reference str will refer to new object,
and reference to old object lost now
*/
Use of StringBuffer or StringBuilder:
StringBuffer class is mutable hence whenever a lot of modifications required on String object use StringBuffer.
StringBuilder class is same as StringBuffer with only difference that methods in StringBuilder are not synchronized hence its not thread safe but runs faster than StringBuffer.
Equals vs '==' for String objects
String s1="abc";
String s2="abc"; // same string literal will be referenced
String s3= new String("abc");
System.out.println(s1==s2); // true same literals in string pool
System.out.println(s1==s3); // false
//since object creation using new operator doesn't point to literal in string pool
System.out.println(s1.equals(s3)); //true,equals method checks contents of objects
Serialization
Serialization is a process by which Object is written to stream and actual object could be re-constructed from that stream.
Primary use of serialization is to construct stream of object,transfer through network and reconstruct over there.Serialization is also useful in Remote method invocation.
Serializable is a
marker interface, without any methods. By implementing Serializable an indication to compiler/JVM sent to handle Java serialization.
SerialVersionUID used to indicate the version of the class and to ensure that the same class is loaded while de-serializing the object.In case any mismatch in SerialVersionUID an InvalidClassException is thrown.
SerialVersionUID is written to the stream while serializing the object, in case there are any changes in class and a new version need to be released change SerialVersionUID to indicate the new version. SerialVersionUID is static final field, though static fields are not related to Object hence not serialized , but in case of SerialVersionUID, it is an exception to above condition.
Collections
Equals and HashCode contract:
case 1:
If x.equals(y) = true then x.hashCode=y.hashCode (Must); similarly
if x.hashCode != y.hashCode then x.equals(y) = false (Must)
Its NOT the same, other way round, i.e.
case 2:
if x.hashCode = y.hashCode then there is no constraint on x.equals(y); similarly
if x.equals(y) = false then no constraint on hashCode.
This concept is very handy, while hashing of an object(HashMap, HashSet etc).
The contract states that if two objects pass equality test then they must land to same bucket hence hashCode must be same.
In case hashCode is not same it will indicate that the objects must land in different buckets, hence objects must fail equality test.
If we talk about case 2: there might be two objects which has same hash code hence land to same bucket(collision) but it may or may not pass equality, since there may exist multiple entry at the same bucket.
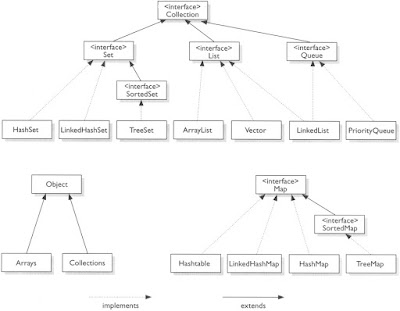
following is a diagram for important interfaces and classes of Collection framework.
1. List : Sequence of elements
2. Set : Collection of unique elements
3. Queue: Things arranged in order in which they are to be processed. (typically first in first out)
4. Map : Stores association between key(uniqueID) and value.
1. List : provides index based access. Implementing classes
1.1 ArrayList : Dynamic arrays which provides fast iteration and fast random access(due to index based implementation), slow insertion/deletion.
1.2 Vector : Same as ArrayList with synchronized methods.
1.3 LinkedList: Doubly linked list implementation, makes fast insertion or deletion but slow iteration.
2. Set : Contains only unique elements
2.1 HashSet : Uses HashMap internally, unordered & unsorted collection of unique elements.
2.2 LinekdHashSet: Ordered version of HashSet
2.3 TreeSet : Sorted version of HashSet
3. Queue : Things arranged in order in which they are to be processed. (typically first in first out)
3.1 PriorityQueue : Creates a queue that is based on the queue's Comparator or natural ordering.
4. Map : Stores association of unique key to values
4.1 HashMap : Stores key value pairs based on hashCode of key, in case of collision a link to previous entry stored and while accessing values hashCode is used to determine actual bucket and then equals method to identify actual value.
4.2 Hashtable : Same as HashMap with synchronized methods.
4.3 LinkedHashMap: Maintains insertion order.
4.4 TreeMap : Sorted Map.
Iterators: General purpose standardized way of accessing elements from collections(though not implemented by Maps)
Comparable interface: Objects of the classes implementing Comparable can be ordered (i.e. TreeSet, sorted collection of unique items) the objects that need to be sorted must implement Comparable interface(sorting requires comparison).
To implement Comparable a class must implement compareTo(Object anotherobj) method which returns an integer as follows:
negative if thisobj < anotherobj
positive if thisobj > anotherobj
zero if thisobj == anotherobj
Comparator interface: Comparable interface requires the class to modify whose instances we need to sort by implementing conpareTo method inside the class.
If a class can't be modified then a separate class can be created which implements Comparator and defines its method compare(Object objone, Object objtwo) which acts same as compareTo method of Comparable.
Generics
Points to note:
1. Generic type safety is for compile time, compiler checks for parametric type safety. After compilation all parameters related to Generic type removed.
2. Generic type is only for Objects, not for primitives.To use primitives, Java uses autoboxing.
3. Mixture of generic and non generic code compiles fine, but a cast is required while accessing objects. Casting may fail at runtime, if its a wrong cast with classCastException.
4. Polymorphic assignments does not work to Generic type, for example:
List < Animal > animal = new ArrayList < Dog >
//polymorphic assignment not allowed.
(assuming Dog is a subclass of Animal)
Threads
A process may contain multiple threads. Threads share same address space while each thread having its own stack,program counter, registers.
To understand more basics about threads check these lecture notes:
Threads Lecture Notes
 |
| Figure: Thread States |
To create a thread in Java either implement Runnable or extend Thread class, implementing Runnable is preferable until unless there is a requirement to override any method from Thread class.
To start a thread call the method start(), calling method run() directly, will not start a new thread.
Java provides locking mechanism for synchronization between threads, each Object in Java has its own lock and each class has a lock(Class lock) associated with it.
Object level lock and class level locks are different, the class has only a single lock.
Access to class's static fields is controlled by a lock that's distinct from the lock for any instance of the class.
Synchronization is achieved by acquiring a lock on object(or class).
Once a thread acquires a lock on an object no other thread can acquire lock on that object,hence only one thread can execute inside the synchronized block.
wait,notify,notifyAll methods defined in Object class, used to signal between threads and must be called from inside synchronized block.
While waiting for a signal,thread releases its lock. Sleeping thread(sleep method call) doesn't releases its lock.
A thread executing notify on an object gives chances to a waiting thread to continue, once the notifying thread releases its lock the waiting thread may acquire the lock and continue.
sleep and yield methods are defined as static methods in Thread class since these methods are applied on a thread rather than on object. wait, notify, notifyAll are applied on a object hence non-static.
volatile keyword is an indicator to compiler to use a variable's value from main memory rather from cached copy of any thread.
Garbage Collection
In Java, memory allocation and de-allocation is handled by JVM, an object without any reference is said to be eligible for garbage collection.
JVM uses mark and sweep algorithm to determine which objects have live references.
This algorithm traverses all object references (object graph) and marks all the objects which have live references. Apart from live objects, all other objects are eligible for garbage collection, so heap memory containing these objects reclaimed.
Marking process is very time consuming in case all the objects need to be scanned, so JVM uses generational garbage collection.
 |
| Figure : GC Generartions |
|
The heap is divided in following sections:
1. Young generation
1.1 Eden space - Part of the heap memory from which memory is initially allocated for most objects.
1.2 Survivor space - Part of the heap memory containing objects that have survived the garbage collection of the Eden space.
2. Old generation(Tenured space) - Part of the heap memory containing objects that have existed for some time in the survivor space.
3. Permanent generation - The pool(non-heap) containing all the reflective data of the virtual machine itself, such as class and method objects. With Java VMs that use class data sharing, this generation is divided into read-only and read-write areas.
When young generation fills, a minor garbage collection performed, surviving objects first moved to survivor space and eventually moved to old generation.
When old generation fills, a major garbage collection is performed.
The permanent generation is included in full garbage collection.
Finalize() method is called before performing garbage collection on an object and it is invoked only once for an object's life-cycle.
In case of any exception in finalize method it is ignored and garbage collection of that object terminates.
Garbage collector is a daemon thread, garbage collection can't be forced but a request can be placed for garbage collection in following ways:
1. Invoking gc() method of Runtime class.
2. Invoking System.gc()