To learn the analysis of algorithms and to dive in the study of
complexity for algorithms few mathematical concepts are required and
used in almost all cases.
I am presenting few concepts in simple manner, so a beginner can grasp it easily and use it in further study of algorithms.
Asymptotic notations:
Big O notation (middle image in above figure):
O(g(n)) = {f(n): there exist positive constants c and n0 such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0}.
It specifies that function gives a upper bound on the complexity of the algorithm and it's the highest value that an algorithm could achieve and not depends on any particular condition, whatever is the input its the highest bound on the time.
whenever we write f(n) = O(g(n)) then f(n) is upper bounded by g(n), it means g(n) is having more value than f(n) or in other words{though not technically correct, we can write value of f(n)<= g(n)}.
Θ-notation :(First image in above fig.)
Θ(g(n)) = {f(n) : there exist positive constants c1, c2, and n0 such that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0}.
function f(n) is sandwiched between g(n) for any two arbitrary constants c1 and c2 such that for any value(eg c1=1/2) f(n) is smaller than g(n) as well as for any other value (eg c2=3/2) f(n) is greater than g(n).
Θ notation is more stronger than O notation and we can write Θ subset of O.
The definition of Θ(g(n)) requires that every member f(n) Θ(g(n)) be asymptotically non-negative, that is, that f(n) be non-negative whenever n is sufficiently large. (An asymptotically positive function is one that is positive for all sufficiently large n.) Basically it is all related to set theory and we denote each set as a set of functions and complexity is based only for positive functions only.
Ω-notation: (Last image in above fig.) :
Ω(g(n)) = {f(n): there exist positive constants c and n0 such that 0 ≤ cg(n) ≤ f(n) for all n ≥ no}.
it means function f(n) is greater than g(n) for a sufficient value of constant c.
Few facts:
floor(x) =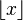 is the largest integer not greater than x and ceiling(x) =
is the largest integer not greater than x and ceiling(x) =  is the smallest integer not less than x.
is the smallest integer not less than x.
for example floor(9.6)=9 and ceiling(9.6)=10.
I am presenting few concepts in simple manner, so a beginner can grasp it easily and use it in further study of algorithms.
Asymptotic notations:
 |
| Asymptotic notations |
Big O notation (middle image in above figure):
O(g(n)) = {f(n): there exist positive constants c and n0 such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0}.
It specifies that function gives a upper bound on the complexity of the algorithm and it's the highest value that an algorithm could achieve and not depends on any particular condition, whatever is the input its the highest bound on the time.
whenever we write f(n) = O(g(n)) then f(n) is upper bounded by g(n), it means g(n) is having more value than f(n) or in other words{though not technically correct, we can write value of f(n)<= g(n)}.
Θ-notation :(First image in above fig.)
Θ(g(n)) = {f(n) : there exist positive constants c1, c2, and n0 such that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0}.
function f(n) is sandwiched between g(n) for any two arbitrary constants c1 and c2 such that for any value(eg c1=1/2) f(n) is smaller than g(n) as well as for any other value (eg c2=3/2) f(n) is greater than g(n).
Θ notation is more stronger than O notation and we can write Θ subset of O.
The definition of Θ(g(n)) requires that every member f(n) Θ(g(n)) be asymptotically non-negative, that is, that f(n) be non-negative whenever n is sufficiently large. (An asymptotically positive function is one that is positive for all sufficiently large n.) Basically it is all related to set theory and we denote each set as a set of functions and complexity is based only for positive functions only.
Ω-notation: (Last image in above fig.) :
Ω(g(n)) = {f(n): there exist positive constants c and n0 such that 0 ≤ cg(n) ≤ f(n) for all n ≥ no}.
it means function f(n) is greater than g(n) for a sufficient value of constant c.
Few facts:
- The constants(c1,c2 etc) mentioned in each case should be only numerical constants and should not be any exponential or any other value , for example :
- f(n) = Θ(g(n)) iff f(n) = O(g(n)) and f(n) = Ω(g(n)) because in that way only it will be upper bounded by g(n) as well as lower bounded by g(n) for any constants c1,c2.
- We generally neglect lower order terms for analyzing the complexity of algorithm. eg( an2+bn+c) could be written as O(n2))
floor(x) =
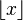 is the largest integer not greater than x and ceiling(x) =
is the largest integer not greater than x and ceiling(x) =  is the smallest integer not less than x.
is the smallest integer not less than x.for example floor(9.6)=9 and ceiling(9.6)=10.
No comments:
Post a Comment